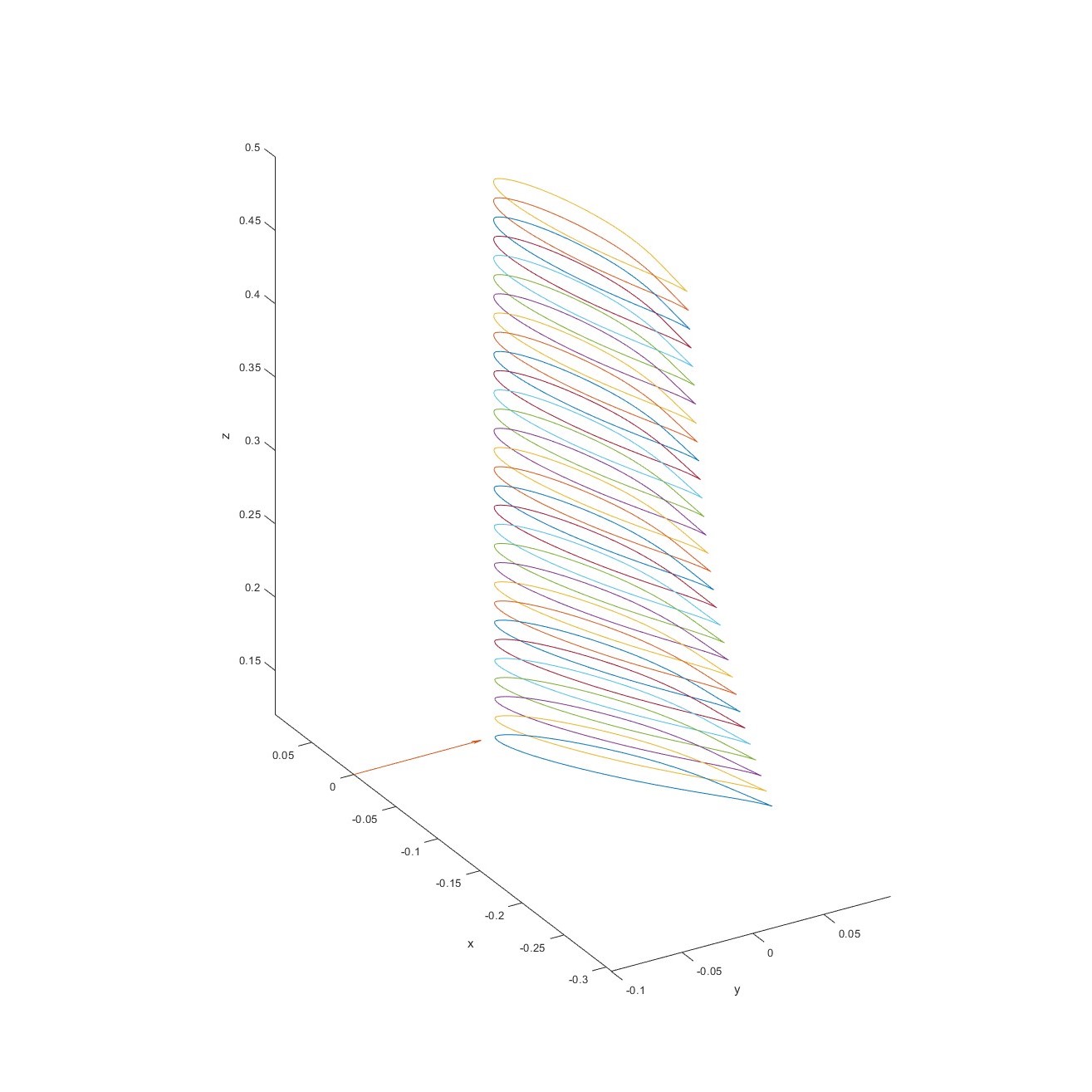
The aim of the project is to determine the optimum blade geometry for a small-scale wind turbine of 500m rotor radius using computational techniques. The project initiated with a full-factorial DoE (design of experiments), followed by a 2-way ANOVA analysis to identify the significance for the factors chosen. I implemented the 4-D Nelder Mead algorithm as the optimisation method for the problem, where the wind turbine blade was modelled mathematically in MATLAB using an iterative solver, based on Blade element momentum theory and aerodynamic lookup tables for S822 blade profile. Optimised blade design was manufactured via fused-filament fabrication and tested in the University of Bath’s wind tunnel with an approximately 3 m/s free stream velocity. The source code for this project can be view on GitHub.
The Project Timeline
Click to reveal details about the process
01
Design of experiment
The objective of this section is identifying the significant design factors that will influence the rotor rpm. Series of factors is to be establish and conduct an experiment. The voltage and current will be measured and tabulated for each combination of factors as part of the analysis to identify the power generated. 2-way ANOVA will be used to identify the significance for the factors chosen.
02
Optimisation process using computational method
This section involved developing an optimisation method for the problem. The Blade momentum theory model was built in MATLAB as a solver. The Nelder-Mead algorithm was developed as the optimiser for the problem. An optimised blade profile was generated at the end of the process
03
Presentation and wind tunnel testing
The optimised blade profile were inputted into Autodesk fusion 360. The blade was then manufactured via fused-filament fabrication and tested in the University of Bath’s wind tunnel with an approximately 3 m/s free stream velocity.
Following the construction of the BEMT model, 4 parameters in which they are considered to be having major influences on the efficiency of the wind turbine were chosen to be optimised and 6 parameters to be kept constant throughout the process.

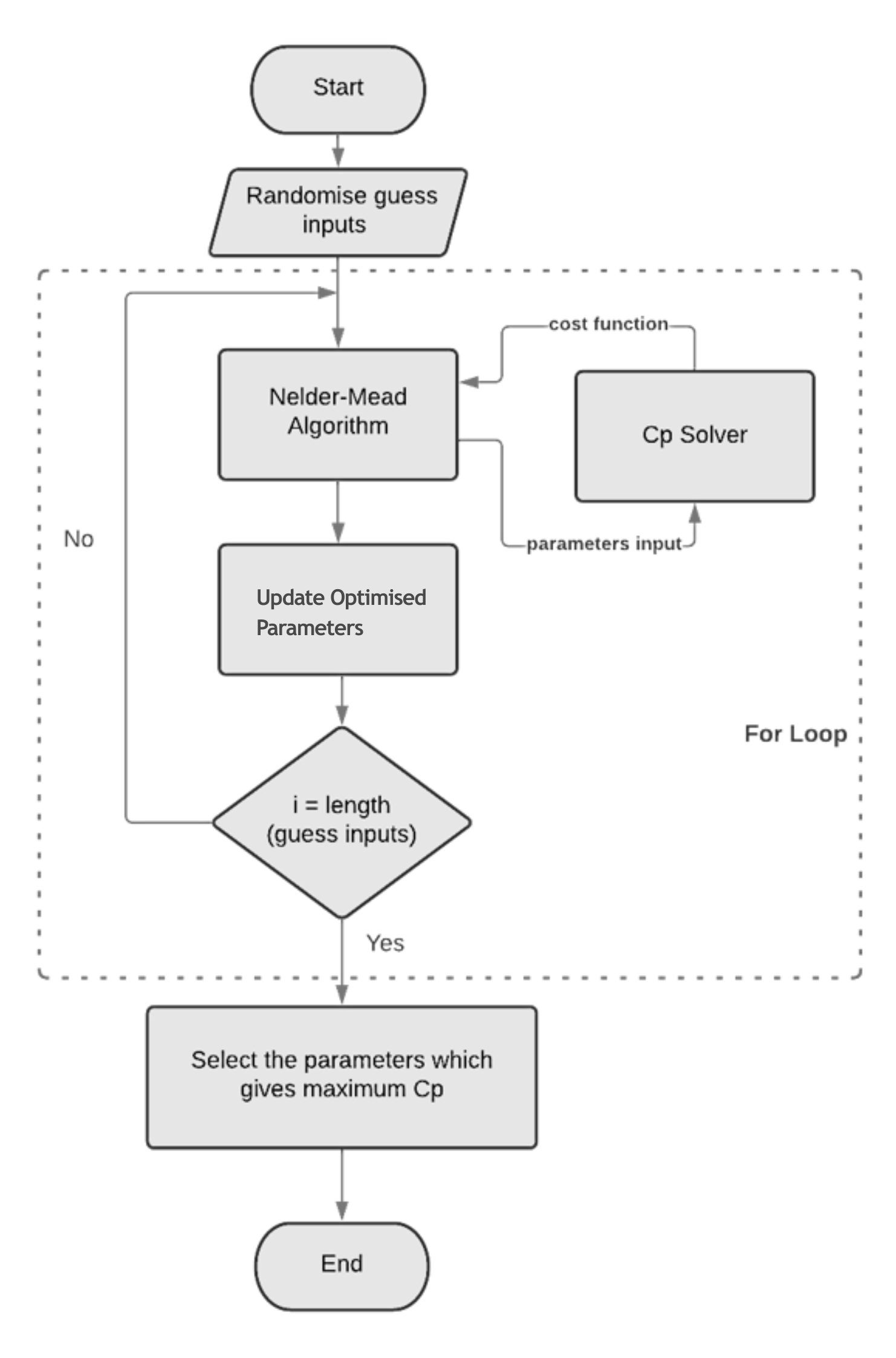
Initial guesses were inputted into the optimiser. The optimiser will then call the solver to retrieve the cost function where it will evaluate the cp value for each iteration. The process will stop as the pre-set number of iterations attained and the optimised parameters is updated.









.png)